Choice Processes

Choice Processes

Update

As interesting as I believe this model to be, it is not an accurate specification of the CSP choice operator. It does explain how the Gang of Four’s composite design pattern translates to Alloy. Please feel free to explore this model; bear in mind that it doesn’t describe what I wanted.

---

Tony Hoare tells us in his book “Communicating Sequential Processes”:

Every process P expressible in the notations introduced so far can be written in the form \((x : B \to f(x))\) where f is a function from symbols to processes, and where B may be empty (in the case of STOP)

He subsequently explains how we could use the functional programming language LISP to implement the beginnings of a CSP interpreter. I enjoy writing code in functional languages, but I am curious to see how to achieve the same in an object-oriented language instead.

This specification describes CSP processes in a manner that facilitates their object-oriented implementation.

Our Approach

CSP is a process algebra. It describes how new processes are created from smaller processes using operators. At this stage, we are concerned with combining prefix processes into indexed choice processes via the choice operator. We shall develop a model of processes that facilitates the discovery of a given process’s menu, whether it is a prefix or an indexed choice. We don’t care how a process is composed when we ask for its menu. All of that motivates us to apply the GoF composite design pattern.

Applying Composite

The composite pattern is described in terms of four participants:

1. Component
2. Leaf
3. Composite
4. Client

Applying it requires us to find meaningful names for each participant. The Alloy we’ll write will contain signatures corresponding to each name. The names I’ve chosen are in the following table.

Participant	Signature
Component	Process
Leaf	Prefix
Composite	Choice
Client	TBC

I am not ready to commit to naming the Client yet, although I suspect it will be an interpreter. For now, it won’t appear in our Alloy specification.

Signatures

Key to modeling in CSP is the idea of an event. Bill Roscoe says in his book “Understanding Concurrent Systems”:

In constructing a process we first have to decide on an alphabet of communicating events – the set of all events that the process (and any other related processes) might use. The choice of this alphabet is perhaps the most important modelling decision that is made when we are trying to represent a real system in CSP.

Clearly, we need to consider events in our model! But at this exploration stage, we shall omit some details and consider events unstructured. As such, we will declare Event as a module dependency.

module Process[Event]

We define Process as an abstract signature. We will associate the composite Menu “operation” with it by declaring a relation of type \(\text{Process} \rightarrow \text{Event}\).

abstract sig Process {
  Menu: set Event
}

Prefix processes are constructed from one Event and one Process. They are typically written \(e \rightarrow P\) where \(e\) is an Event and \(P\) is a Processs. Prefix objects are the leaves of our hierarchy.

sig Prefix extends Process {
  , head: Event
  , body: Process
}

The composite structure in our hierarchy is the Choice. It is a collection of prefix objects, which we will model using a relation of type \(\text{Choice} \rightarrow \text{Prefix}\).

sig Choice extends Process {
  , Child: set Prefix
}

Now, we must consider which constraints to apply to our structures so they combine in a way we can recognise as having something to do with CSP. I’m not a fan of using facts in my models. I find they get in the way when we transition from static to dynamic modelling. We’ll be using predicates instead.

Predicates

I’ve already constrained the model by how I’ve written the signatures. In particular, the head and body relations have been defined as functions; that is, they are both simple and entire. But as it stands, this specification will find instances that do not model CSP processes. To see what I mean, you can run the following command:

run {} for 5

Browse the instances, and you’ll soon find structures that cannot be interpreted as CSP processes. For example:

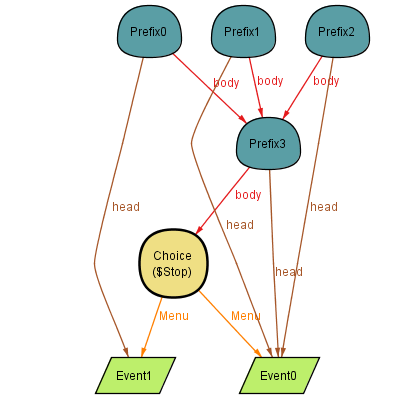
It is essential to understand that if we were to jump into implementation and create classes based on these unconstrained signatures, we would be building software capable of representing the instance above, among other horrors.

We’ll work inwards from the leaves of our hierarchy by first describing the structure of Prefix processes and how they contribute to the Menu relation.

Prefix

For Prefix objects, the Menu and head relations coincide.

pred prefix_menu {
  Prefix<:Menu = head
}

Prefix objects are considered equal when they share the same head and body.

pred prefix_identity {
  Prefix<:iden =
    head.~head & 
    body.~body
}

Choice

For Choice objects, the Menu relation combines the Menu of its children.

pred choice_menu {
  Choice<:Menu = Child.Menu
}

Two Choice objects are identical exactly when their Child relations coincide.

pred choice_identity {
  all z,y: Choice {
    z = y iff z.Child = y.Child
  }
}

The pointfree version of choice_identity is

\[\frac{\text{Child}}{\text{Child}} \subseteq \text{id}_\text{Choice}\]

Sadly, Alloy lacks syntax for division operators, so we must resort to quantifiers. I find that upsetting.

Stop

A Choice without a Child is called a Stop.

pred stop(c: Choice) {
  no c.Child
}

fun Stop : set Choice {
  { c: Choice | stop[c] }
}

Because of the way we have defined the identity on Choice objects, Stop will have only one inhabitant. So, we may speak of the Stop object.

Commands

We are in a position to generate instances which model CSP Prefix and Choice processes:

run {
  prefix_menu
  prefix_identity
  choice_menu
  choice_identity
} for 5

We could combine that four-fold conjunction into another predicate, but I don’t see any real motivation for doing so now.

Next Steps

With the completion of our static model, we must now focus on the dynamics of process creation. We’ll do that in another post.